Moments d'inerties...
Moments d'inerties... - Aide aux devoirs - Emploi & Etudes
Marsh Posté le 21-07-2007 à 21:07:31
en fait ils vont dépendre de z
donc c'est possible que tu ne puisses pas expliciter le calcul
Marsh Posté le 21-07-2007 à 21:12:03
Mwai, pour Izz : (x²+y²)=r² simplife beaucoup les choses. Les x²+z² ou y²+z² , c'est une autre paire de manche ![]()
En fait je me demande si il n'y a pas une astuce comme pour un disque : 
Marsh Posté le 21-07-2007 à 21:16:29
réfléchis à ce que ça représente de faire tourner un disque autour de Ox, Oy ou Oz
puis ton cylindre autour de Oz
et maintenant ton cylindre autour de Ox et Oy...
normalement tu devrais comprendre pourquoi t'arrives pas à calculer le moment d'inertie correspondant
d'ailleurs qui te demande de faire ce calcul ?
Marsh Posté le 21-07-2007 à 21:32:06
Je reste persuadé qu'il y a un moyen (sinon on ne me le demandrait pas ![]() ), et c'est dans le cadre d'un cours de Méca, c'est un des anciens examens que j'essaye de faire/comprendre.
), et c'est dans le cadre d'un cours de Méca, c'est un des anciens examens que j'essaye de faire/comprendre.
Marsh Posté le 21-07-2007 à 21:38:57
au temps pour moi en fait
le calcul n'est pas très compliqué
fais d'abord le calcul pour un cylindre plein
ensuite tu raisonneras par additivé avec un cylindre de masse volumique mu et rayon R2 et un autre de masse volumique (-mu) et rayon R2
![]()
edit : bon par contre c'est la matrice d'inertie au centre du cylindre que tu auras, après si tu veux l'avoir en tout point il faudra encore quelques lignes de calcul
Message édité par Profil supprimé le 21-07-2007 à 21:41:04
Marsh Posté le 21-07-2007 à 21:50:34
Je peux pas garder les cordonées cylindrique pour Ixx et Iyy ? C'est plus simple de repasser en c. cartesiennes vu que le r²=x²+y² ne joue plus, non ?
Ou alors, je peux simplement faire ça ? 
( C'est Iyy )
C'est juste ?
Message édité par XamamaX le 21-07-2007 à 23:00:12
Marsh Posté le 22-07-2007 à 18:07:04
ReplySujets relatifs:
- Souvenirs, moments inoubliables pendant vos études.
- Vos meilleurs moments en entretien
- Le topic des entretiens

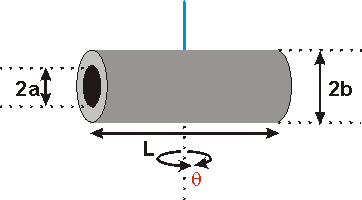
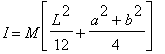
Marsh Posté le 21-07-2007 à 21:04:47
Bonjour à ceux qui passeraient encore par ici,


Je cherche à déterminer les composantes du tenseur d'inertie d'un tuyeau de hauteur H, de masse volumique mu, de rayon interne R1 et de rayon externe R2...
Pour Izz, ça va...
Je ne vois par contre pas comment faire pour les autres axes ( Ixx et Iyy) ... je sais qu'ils seront identiques par symétrie mais j'arrive pas à trouver l'intégrale à faire
Un ptit coup de main serait le bien venu....
Message édité par XamamaX le 21-07-2007 à 21:05:03