Augmenter d'une distance un polygone
Augmenter d'une distance un polygone - Algo - Programmation
Marsh Posté le 03-04-2018 à 15:27:05
L'algorithme générique n'est pas trivial. Les mots-clés que tu veux chercher sont: inward outward polygon offsetting
Pour un truc générique, il faudra sortir l'artillerie lourde. J'étais intéressé par un problème un peu plus simple: étant donné un polygone, pouvoir dessiner ce polyone avec une épaisseur de trait variable. Dans ce cas, il y avait pas mal de simplifications, au prix que certaines surfaces pouvaient être redessinées plusieurs fois.
Maintenant partir d'un polygon fermé et étendre/restreindre sa surface, implique la création/suppression de segments/points.
J'avais regardé la bibliothèque clipper, écrite en C# sous license MIT, très générique et rapide. Mais, c'était beaucoup trop compliqué pour ce que je voulais faire. À l'origine c'est fait pour du découpage (clipping) de polygone, mais elle a aussi des fonctions pour étendre/restreindre la surface.
Marsh Posté le 03-04-2018 à 21:00:21
| rufo a écrit : J'étais parti sur le calcul du centre de gravité de la forme, de définir un axe centre de gravité / sommet et de rajouter la distance sur ce axe, me permettant ainsi de définir les coordonnées des sommets du polygone agrandi, en me disant que le polygone augmenté aurait le même centre de gravité. Mais ça ne marche pas |
Salut, j'aurai fait de même, tu es sûr que ça ne marche pas ?
Enfin j'aurai fait très légèrement différemment, mais je pense que c'est ce que tu as voulu dire. Je calcule le centre de gravité puis j'augmente la distance du centre de gravité jusqu'au sommet d'un coefficient multiplicateur puisqu'on parle d'une homothétie. Toi tu dis ajouter, moi je dis multiplier, car évidemment si tu ajoutes la même distance pour tous les couples centre de gravité - sommet ça ne fonctionnera pas. Je pense que tu as juste mal formulé, mais sait-on jamais si ça peut aider...
Si tu as multiplié je suis quand même étonné que ça ne fonctionne pas, car pour moi c'est la définition d'une homothétie. Alors peut-être vérifier qu'aucune erreur ne c'est glissée.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 03-04-2018 à 23:03:50
Je parle bien d'ajouter une distance à chaque sommet du polygone, sur un axe centre de gravité/sommet mais ça déforme le polygone de base, donc ça ne fonctionne pas comme je voudrai. Ca marcherait, je pense, si le polygone est strictement convexe. Mais avec des arêtes concaves, ça fout tout en l'air ![]()
J'ai fait des recherches et me suis rendu compte que ce pb était loin d'être simple. Je suis parti sur des mots-clés genre algorithm offset polygon outside :
https://stackoverflow.com/questions [...] g-polygons
https://math.stackexchange.com/ques [...] offsetting
http://www.ics.uci.edu/~goodrich/pubs/tol-cgta.pdf
Le lien sur Stackoverflow m'a l'air intéressant. En revanche, le dernier lien (le pdf) m'a l'air assez overkill ![]()
Après, comme c'est à dessiner dans google earth, j'ai la joie des calculs de coordonnées connaissant un point d'origine, un azimut et une distance à ajouter à me taper, mais bon, là, j'ai trouvé les formules de trigo (merci internet, sans ça, j'étais mort ![]() ) :
) :
http://www.movable-type.co.uk/scripts/latlong.html (la partie "Destination point given distance and bearing from start point" )
Pour ceux que ça intéresse, le calcul du centre de gravité d'un polygone irrégulier, j'ai trouvé un très bon site qui donne la formule est le détail des calculs sur un exemple. Ca permet de bien de tout vérifier en cas de bug : http://math.15873.pagesperso-orange.fr/page9.htm
Jeudi, je vais tester ce que ça donne...
Edit : un autre article intéressant sur le sujet : http://vmk.ugatu.ac.ru/c%26p/artic [...] in2007.pdf
Message édité par rufo le 05-04-2018 à 10:18:26
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 17:16:51
Bon, j'ai réfléchi sur papier et je pense avoir trouvé un algo pas trop compliqué qui a de bonnes chances de fonctionner dans la plupart des cas.
Je considère que mets sommets sont ordonnés (sens horaire ou anti-horaire, ça n'a pas d'importance).
Pour chaque sommet Si Faire
1) Calculer l'angle Ai que forment les sommets Si-1, Si et Si+1
2) calculer la droite passant par le sommet Si et formant un angle Ai/2 avec le segment [Si-1;Si]
3) calculer les 2 points situés à la distance D par rapport au sommet Si et situés sur la droite précédemment calculée (oui, ça ce stade, j'ignore de quel côté le point doit se trouver pour être correct).
4) conserver le point qui permet d'obtenir une aire supérieure à l'aire du polygone initial quand je prends tous les sommets du polygone initial excepté le sommet Si et que je prends à sa place l'un des 2 points calculés.
Fin pour
Relier les points calculer entre eux pour former le polygone agrandi.
Ca m'a l'air jouable.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 17:42:57
J'avoue ne pas bien comprendre ce que tu veux faire, pour moi l'homothétie fonctionne :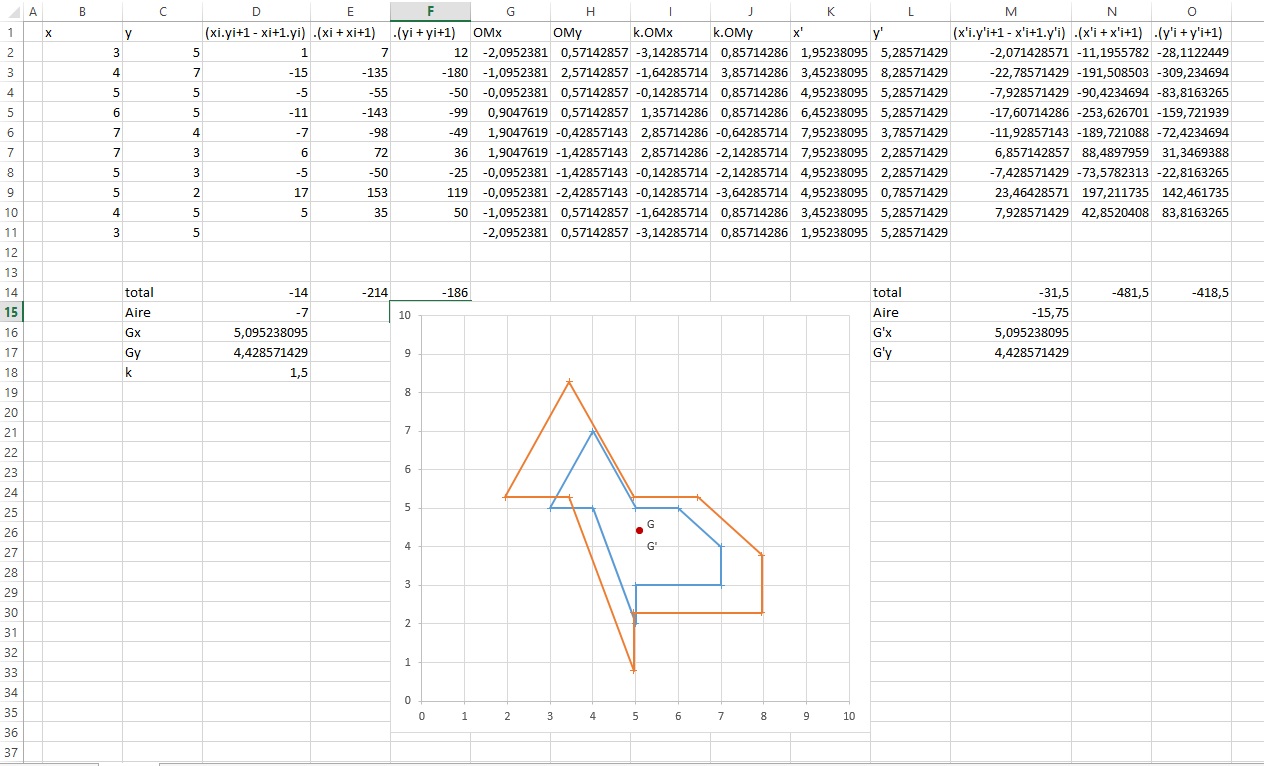
Je n'ai pas tenté de polygone croisé car c'est plus difficile à visualiser mais je ne pense que ça change grand chose, je ne trouve pas de cas où ça ne fonctionne pas.
Après si tu ne veux pas de croisement entre la version normale et la version agrandie alors il faut transformer ton polygone agrandi mais là c'est à toi de voir ce que tu veux comme modèle approché.
Par exemple là j'ai fait en sorte de déplacer chaque point d'une certaine distance vers l'extérieur suivant la bissectrice de l'angle formé par chaque côté du point :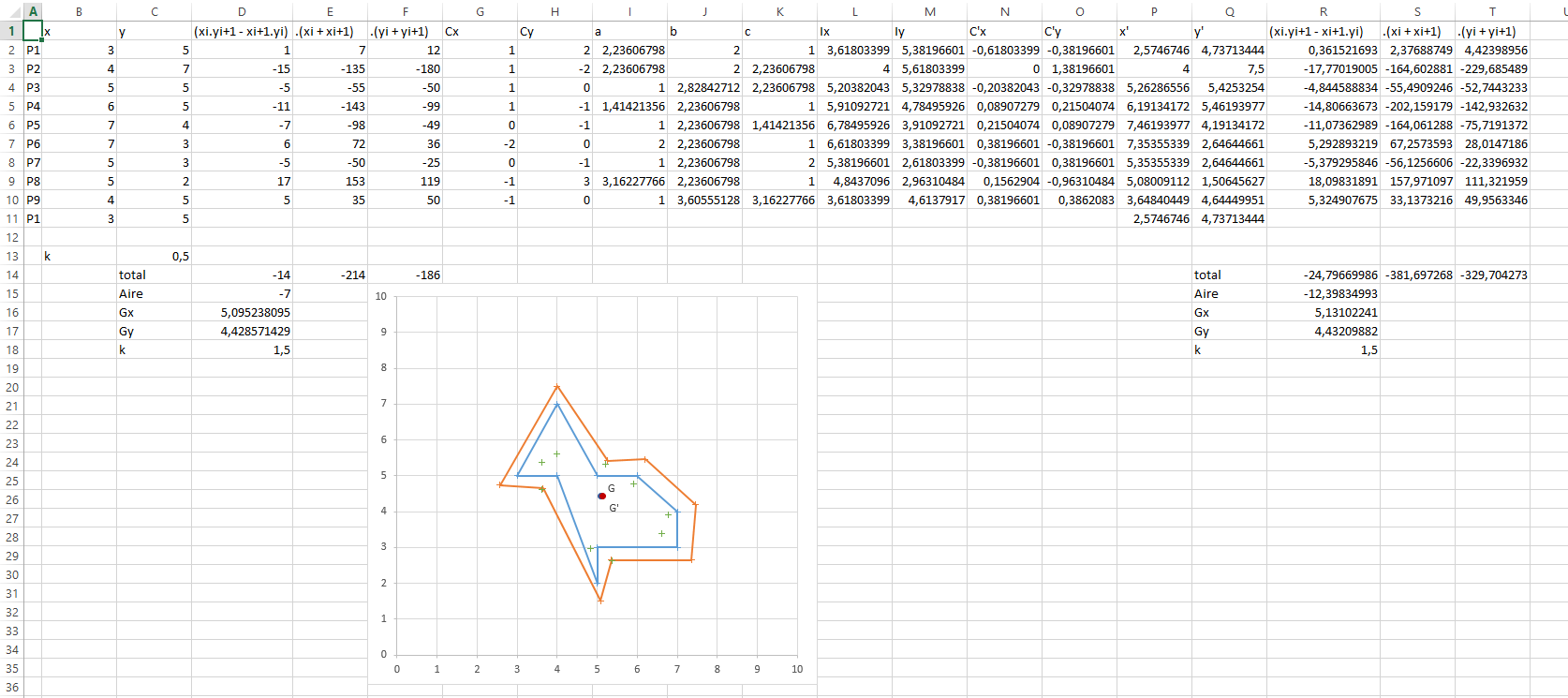
Tu peux aussi t'amuser à tracer les parallèles et placer les points aux intersections.
Message édité par MaybeEijOrNot le 04-04-2018 à 17:44:55
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 04-04-2018 à 18:03:14
C'est bien un truc dans le genre de ton 2ème cas. Effectivement, je ne veux pas que le polygone initial et celui obtenu se croisent.
T'as eu la même idée que moi avec les bissectrices (cf l'algo de mon dernier post).
Par rapport à ta dernière remarque, je pense que tu fais référence aux parallèles aux arêtes du polygone. C'était mon autre solution.
La spec qu'on m'a filée n'est pas très précise sur la notion d'ajout d'une distance à un polygone : on ajoute cette distance à une arête ou à un sommet.
Peut-être que la solution ultime est une combinaison des bissectrices pour avoir une distance D ajoutée aux sommets et des parallèles aux arêtes séparées elles aussi d'une distance D.
Edit : juste par curiosité, quel critère as-tu choisi pour déterminer lequel des 2 points sur la bissectrice faut-il conserver ? Moi, j'ai choisi le critère de l'aire.
Message édité par rufo le 04-04-2018 à 18:04:51
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 18:28:57
Ta version ultime, j'y ai pensé aussi, mais normalement tes parallèles aux arêtes se croisent justement sur la bissectrice si je ne dis pas de connerie, et évidemment deux droites ne se coupent qu'une fois donc tu ne peux pas faire varier deux paramètres (cf. distance entre deux parallèles et distance entre le sommet et celui sur l'arête).
Sinon pour la choix du point à garder en fait j'ai fait manuellement pour ne pas m'emmerder mais je suppose qu'il faut calculer l'angle entre les deux arêtes et quand l'angle est obtus tu changes le signe dans le calcul de tes nouvelles coordonnées.
EDIT : arf non, si tu calcules les angles avec Al-Kashi tu ne vois pas les angles obtus ou aiguës. Je vais tenter de réfléchir au problème.
Message édité par MaybeEijOrNot le 04-04-2018 à 18:35:17
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 04-04-2018 à 18:42:57
Moi, je pense l'avoir résolu avec l'aire. J'ai l'aire de mon polygone initial qui vaut A0. Au sommet Si, pour savoir lequel des 2 points Pi1 et Pi2 je dois conserver, je calcule l'aire des 2 polygones formés par les sommets S1, S2...Pi1, Si+1, Si+2...Sn et par les sommets par les sommets S1, S2...Pi2, Si+1, Si+2...Sn, ce qui me donne les aires Ai1 et Ai2. Si Ai1 > A0 alors je garde le point Pi1 pour le sommet Si; sinon, je garde le point Pi2.
Ca a l'aire d'être un bon critère. J'ai regardé sur des polygones concaves ou convexes : ça a l'air de marcher à chaque fois (sur le papier en tout cas).
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 18:54:52
Oui c'est certain que ça fonctionne de maximiser l'air.
Je cherche néanmoins s'il n'y a pas une solution moins gourmande en fonction de la position du nouveau sommet par rapport à l'ancien et le centre de gravité.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 04-04-2018 à 19:30:21
J'ai exploré la piste du centre de gravité en calculant la distance [centre de gravité; Pi1] et [centre de gravité;Pi2] et de prendre la plus grande. Mais ça marche pas dans le cas de polygones où le centre de gravité se trouve en-dehors du polygone.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 21:41:14
Bon je n'ai pas trop eu le temps de chercher.
Même si il se trouve à l'intérieur ça ne fonctionne pas forcément non plus.
Deux pistes à évaluer : la distance ancien sommet - centre de gravité doit être plus faible que nouveau sommet - centre de gravité.
Sinon on peut déterminer que l'angle est obtus quand le sommet du triangle pointe vers l'intérieur et donc que la base du triangle est en dehors du polygone.
Et ben en écrivant le message, je peux déjà dire que la première piste est fausse. ![]()
Attention aussi, je ne sais pas comment tu calcules tes coordonnées des nouveaux points sur la bissectrice, moi j'utilise les coordonnées du vecteur de la bissectrice. Et si l'une des coordonnées est nulle alors ça implique une division par 0. Si les coordonnées en x du vecteur sont nulles alors pour le calcul (addition d'un vecteur colinéaire de la taille qui va bien) des coordonnées en x de mon nouveau sommet je dois diviser par 0. De même pour les y. J'ai donc juste mis un IF pour vérifier si on a une coordonnée nulle et dans ce cas là on utilise la coordonnée de notre sommet d'origine.
Sur la technique des arêtes parallèles, c'est plus intuitif au niveau du rendu, mais dès lors où tu as des angles très obtus ou très aigües tu as un nouveau sommet qui se retrouve très rapidement à perpète de l'ancien. Tu crées alors des arêtes disproportionnées par rapport à celles d'origines (de très longues dans le premier cas et de très courtes dans le second cas).
Tu es sûr que tu ne peux pas plutôt faire une homothétie ? Car j'ai du mal à voir l'intérêt de faire un "faux" agrandissement d'un polygone.
Message édité par MaybeEijOrNot le 04-04-2018 à 21:43:13
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 04-04-2018 à 21:58:35
Non, l'homothétie n'est pas la bonne solution. Ta figure montre bien pourquoi : le polygone initial n'est pas complètement à l'intérieur du nouveau.
Je ne peux pas expliquer le contexte exact. Je peux juste dire qu'il s'agit de zones géographiques qu'on doit augmenter d'une certaine marge (une distance de quelques centaines de mètres à quelques km). D'où la contrainte que le polygone initial doit être à l'intérieur complètement du nouveau polygone.
Merci pour tes remarques sur les calculs. J'ai déjà eu à traiter ce genre de cas de la division par 0 pour le calcul de la pente de la droite. Ca se résout soit par un IF soit en passant par les équations paramétriques.
Pour les nouveaux sommets trop loin, on peux déformer le polygone en limitant la distance entre le nouveau sommet à l'ancien à la distance D qu'on a ajoutée aux arêtes. Du coup, ça écrête les sommets trop "pointus". D'où pourquoi je proposais de combiner les 2 algos : bissectrices + arêtes parallèles.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 04-04-2018 à 22:15:02
Oui si tu écrêtes tu rajoutes carrément une arête, donc là tout dépend vraiment de l'application.
Si j'ai le temps je parcourrais la piste du sommet du triangle mais je ne garanti rien.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 05-04-2018 à 18:15:55
Bon, j'ai testé en faisant juste les bissectrices. Ca donne des résultats pas trop mal. Je vais par contre devoir gérer les cas où la distance ajoutée fait que des sommets vont se croiser.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 05-04-2018 à 20:56:07
Je n'ai pas eu le temps de réfléchir au problème aujourd'hui mais ce cas arrive aussi avec la technique des parallèles, et dans l'absolu dès lors où tu fais autre chose qu'une homothétie tu vas changer les angles et/ou les proportions et donc conduire à la possible disparition de sommets.
Par contre là tu vas encore bien augmenter la complexité de ton algo. Tu ne pourras pas simplement vérifier que ton arête ne croise pas ses voisines entre ses sommets (d'ailleurs tu ne dois pas pouvoir croiser deux arêtes voisines entre leurs sommets puisqu'elles se croisent déjà en leurs sommets). Tu devras vérifier qu'elle ne coupe aucune des autres arrêtes entre ses sommets. Et dans le cas où il y a croisement il va surement falloir recalculer de nouveaux sommets, refaire des bissectrices, remaximiser les sommets. Au passage tu crées possiblement un polygone creux mais cela ne doit pas changer grand chose au traitement. ![[:psywalk] [:psywalk]](https://forum-images.hardware.fr/images/perso/psywalk.gif)
EDIT : ah si le polygone creux ça change l'ordre des points (d'ailleurs ça crée carrément deux groupes de points) et le calcul d'aires et donc celui du centre de gravité.
EDIT2 : ah mais tu n'utilises probablement plus le centre de gravité, mais tu as toujours besoin du calcul d'aire pour maximiser mais là c'est assez simple, il suffit de faire le traitement de deux polygones distincts, mais tu chercheras à maximiser l'aire du polygone extérieur et minimiser l'aire du polygone intérieur.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 06-04-2018 à 11:24:41
Effectivement, je n'utilise plus le centre de gravité.
Pour le pb de croisement de sommets, je peux détecter si l'intersection de 2 bissectrices (pas forcément celles de sommets connexes) est situé à une distance D' des 2 sommets concernés < à ma distance D que j'ajoute au polygone. Si c'est le cas, une solution "pas trop mal" serait de calculer la bissectrice de l'angle formé par les 2 bissectrices et d'ajouter à distance manquante.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 06-04-2018 à 20:07:19
Perso je serai parti sur un nouveau sommet là où se croisent les arêtes du polygone agrandi. Et du coup je calculerai l'intersection des arêtes et non des bissectrices et de la distance d'offset.
En ne travaillant que sur l'agrandissement.
Si une arête croise une autre entre leurs sommets alors on supprime les sommets entre et on en crée un nouveau au niveau de l'intersection.
Si deux arêtes contigües croisent une même arête alors on forme un polygone "creux", on supprime le sommet des deux arêtes contigües et on crée un nouveau à chaque intersection. On sépare la figure en deux polygones, sur le polygone externe on maximise l'aire, sur le polygone interne on minimise l'aire.
Dans ta solution je ne comprends pas comment tu détermines la "distance manquante" à part à la limite l'intersection des deux bissectrices.
Message édité par MaybeEijOrNot le 06-04-2018 à 20:08:14
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 06-04-2018 à 20:27:44
Moi non plus je ne sais pas comment je détermine la distance manquante ![]()
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 06-04-2018 à 23:09:20
Exemple : 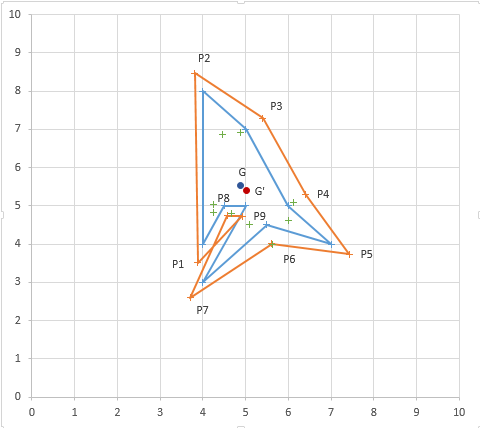
Ici je supprime P8 et P9 et je crée un nouveau sommet au niveau de l'intersection.
Donc comme avant tu calcules ton polygone agrandi en maximisant l'aire pour placer tes sommets du bon côté de chaque bissectrice.
Tu vérifies s'il y a intersection de chacune de tes arêtes avec une autre arête (sans faire le calcul inutile pour les deux arêtes voisines). Si plus de deux arêtes se croisent, vérifier si des arêtes contigües sont impliquées. Sinon tu supprimes les sommets entre les arêtes impliquées et tu crées un nouveau au niveau de l'intersection.
Pour l'instant je ne crois pas qu'il y ait besoin de magie de noire. ![]()
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 07-04-2018 à 11:00:23
J'ai discuté avec le gars qui m'a fait la spec hier pour savoir comment il voulait précisément augmenter son polygone. Dans le cas où ds arêtes se croise, en fait, je pense pouvoir carrément supprimer celles qui posent pb, sans même créer de nouveau sommet.
Il m'a montré un soft qui avait un pb similaire à traiter : eux, il sont passé par des cercles de centre des sommets et ils tracent une tangente aux 2 cercles des sommets connexes. Si des cercles se coupent, ils prennent comme nouveaux points les intersections des cercles (celles extérieures au polygone de départ).
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 07-04-2018 à 12:36:40
Cela me semblait une bonne idée à première vue, mais ça ne semble pas coller avec le cas que j'ai présenté hier : 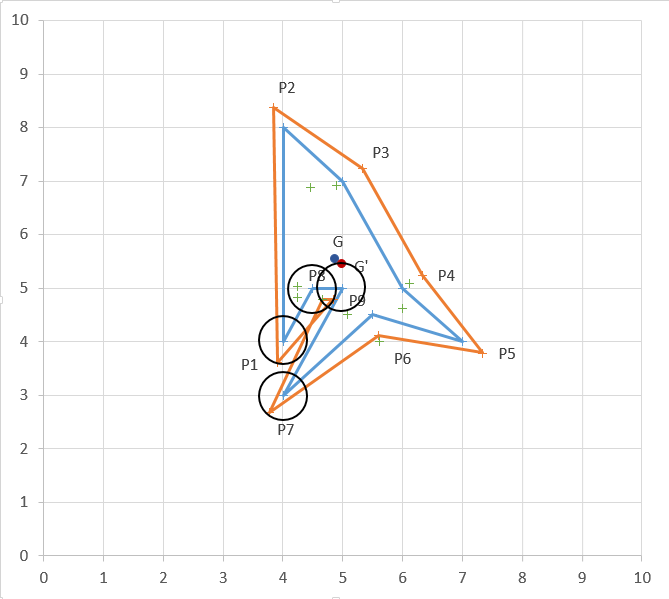
Les cercles P1 et P7 ne se croisent pas. Et sinon l'histoire des tangentes, ça revient à tracer des parallèles.
C'est un peu chargé et fait à l'arrache : 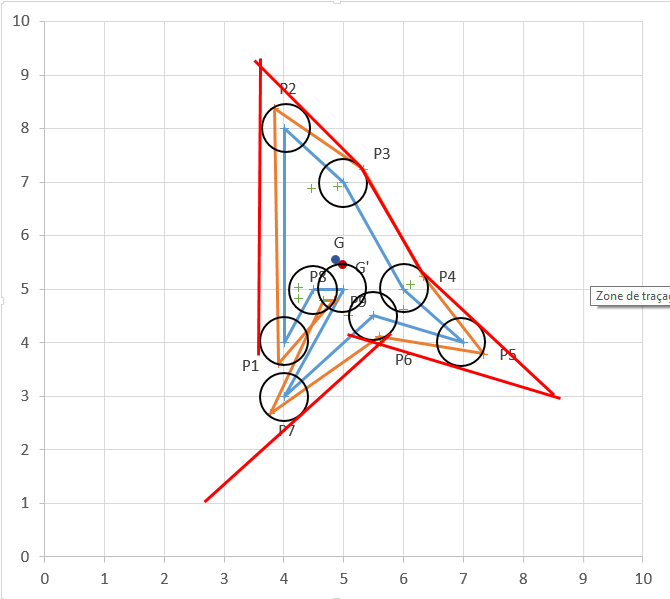
Entre P1 et P7 je ne vois pas ce qu'il faut faire.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Marsh Posté le 07-04-2018 à 13:29:03
P2, il faut arrêter les tangentes de P1 et P2 au cercle centré sur P2. Du coup, ça fait un polygone avec un arrondi aux sommets "trop" convexes.
Pour P1 et P7, il faut tracer une tangente entre les 2 cercles et ignorer P8 et P9.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta
Marsh Posté le 07-04-2018 à 13:51:48
Je ne vois pas comment tu arrives à la conclusion qu'il faut ignorer P8 et P9 en fait, mais si toi tu comprends c'est l'essentiel.
Mais sinon cette technique des cercles est un bon compromis pour appliquer les parallèles puisqu'en effet tu arrondies les angles plutôt que d'aller jusqu'aux intersections qui auraient créées des arêtes disproportionnées.
---------------
C'est en écrivant n'importe quoi qu'on devient n'importe qui.
Sujets relatifs:
- Un free basic qui permette d'augmenter la taille de police facilement?
- Augmenter la luminosité des image (par defaut ou overlay) sous Firefox
- SVG - Faire un scale mais préserver une partie du polygone
- Shell controlable à distance avec socket
- la distance de levenshtein pour calculer le nombre d'apparition dans u
- Distance entre deux objets
- Mon serveur Nas veut pas récupérer le contenu du dossier à distance ?
- Aide Programme Distance
- Création de site (Vente à distance)
- [KML] Comment tranformer un polygone 2D en 3D?

Marsh Posté le 03-04-2018 à 13:39:05
Bonjour,
J'ai un polygone de forme quelconque affiché dans Google Earth. Je voudrais faire grossir ce polygone d'une certaine distance qu'on ajouterait à chacune des arrête du polygone. J'étais parti sur le calcul du centre de gravité de la forme, de définir un axe centre de gravité / sommet et de rajouter la distance sur ce axe, me permettant ainsi de définir les coordonnées des sommets du polygone agrandi, en me disant que le polygone augmenté aurait le même centre de gravité. Mais ça ne marche pas
Mon autre idée c'est de calculer le vecteur normal de chaque arrête et de lui donner comme longueur, la distance à ajouter. Mais ça me paraît compliqué : il n'y aurait pas plus simple ?
Merci par avance.
---------------
Astres, outil de help-desk GPL : http://sourceforge.net/projects/astres, ICARE, gestion de conf : http://sourceforge.net/projects/icare, Outil Planeta Calandreta : https://framalibre.org/content/planeta-calandreta