Elements Finis : Assemblage matrice
Elements Finis : Assemblage matrice - C++ - Programmation
Marsh Posté le 18-11-2012 à 19:38:30
Salut,
Je ne suis pas du tout expert dans le domaine mais ça ressemble à une écriture ou ta matrice de rigidité n'est pas symétrique (me trompe je?)
le vecteur xi tes coordonnées dans l'espace de référence d'où l'apparition du jacobien entre espace de ref et espace réel.
Il faut calculer la matrice de rigidité de chaque éléments contenant N degrés de libertés (qui dépend du problème) noté 1, 2, 3, ... localement et i, j, k dans le problème global (il n'y a pas d'ordre entre i, j et k) (allant de 0 à 25 dans ton cas).
Ensuite il faut sommer les matrices de rigidité élémentaires m de telle façon à ce que M_ij=somme(m_ij) et là tu obtiens la matrice de rigidité globale tu lui applique les conditions aux limites
Et si tu peux poster ton code (ou juste une portion) ça m'intéresse de le travailler avec toi
Salut
un exemple en 1D
http://fr.scribd.com/doc/51933382/ [...] e-rigidite
---------------
A Vendre
Marsh Posté le 22-11-2012 à 20:31:30
Merci pour ta réponse,
La matrice de rigidité est bien symetrique. En fait, j'ai un peu triché sur le titre, je ne fais pas de MEF mais une méthode qui s'appelle Isogeometric method qui est basée sur les NURBS et les surfaces de bezier ... et qui sera surement la nouvelle MEF dans 10 ans vu les résultats obtenus.
Marsh Posté le 26-12-2012 à 15:47:49
Je ne connais pas concretement les methodes concernant les NURBS, mais d'apres ce que tu decris, ca ressemble beaucoup a la FEM. L'idee de FEM est que tu as un maillage global, decoupe en plusieurs element petit ressemblant et regulier. Alors de la, il y a deux matrice de ridigite a construire : matrice de rigidite globale decrivant la propriete intrinseque de ton entier systeme, et les matrice de rigidite locale, decrivant la propriete de chaque element. Il faut avoir une topologie pour pouvoir faire l'assemblage. Cette topologie est en gros l'indexation des points, et l'ensemble des indices qui font des elements. Par example tu as un maillage de 20 neuod, chaque element est un spline composant de 2 noeud, alors la topologie est l'ensemble des element
[0,5]
[6,7]
[5,2]
[3,19]
...
constituant des elements. Sachant qu'une fois finis la parti de modelisation (autrement dit mathematique), tu devra savoir donner toutes les matrices local. L'assemblage se fera par la suite en iterant les elements de topologies, et ajoutant sa valeur dans l'indice correspondant du container des DOFs.
Mais globalement, l'algorithme est tellemenet complique que sans outil d'edition latex, c'est impossible d'expliquer (deja avec les explication complete, c'est difficile a voir).
Le point crucial a comprendre est que la matrice de ridigite est concretement une forme bilineaire de l'integration de deux fonction interpolation (la valeur a l'indice ij est souvent une integration de i-eme Phi et j-eme Phi avec un facteur multiplicative constant). Pour que tout soit clair, il faudra que tu expose toute tes interpolation sur un element generique.
Marsh Posté le 10-03-2014 à 10:04:20
Bonjour, j'espère trouver chez vous la réponse car j'ai pas trouvé où la postée.
J'ai une poutre (ij) qui a des appuis élastiques rotationnelles aux extrémités (l'appui a une rigidité rotationnel "k" ) . Quelles sont les conditions aux limites à donner (pour les déplacements et les efforts) quand on résout son équation différentielle (EI* y''''(x)=0)
Sujets relatifs:
- Quadrature de Gauss sur une matrice
- comment recupurer les valeurs d'une matrice dans une classe exterieur
- matrice vectore rechairche
- somme des éléments d'un tableau
- matrice inverse 4x4 en c
- decaler une matrice vers le haut
- fonction qui transforme une matrice en vecteur en langage C
- VBA : Transférer une matrice dans un tableur Excel
- extraction sous matrice
- matrice en c

Marsh Posté le 15-11-2012 à 12:25:28
Bonjour,
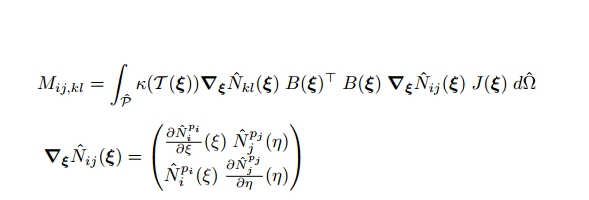
Je cherche à assembler une matrice afin d'obtenir un system classique AX=B. Mon X et mon B sont de dimension 25. Et donc mon A devrait etre de dim 25x25. Seulement comme montré dans l'image ma matrice est une multiplication de matrice 2x2 (les derivees de N et meme les jacobienne) et je ne sais pas comment assembler ... Vous pourriez m'aider ?
Bien cordialement
---------------
http://www.jppanaget.com