Algorithme pour la FFT
Algorithme pour la FFT - Java - Programmation
Marsh Posté le 20-12-2007 à 16:48:56
Bonjour,
Tu cherches quelque chose de bien spécifique, toutefois, je pense que le meux c'est que tu developpe un prog en fonction du modele de calcul de la FFT.
A mon avis, regarde comment est fait le calcul de la FFT sur les oscillos, je c que c tres rapide dans certains cas.
Bon courage, je ne pourrais peut etre pas bcp plus t'aider
Marsh Posté le 20-12-2007 à 16:56:03
je cherche juste à faire une fft... il n'y a pas grand chose de spécifique
une fois que j'aurais les coefficients je devrais pouvoir identifier le pic à 50Hz et calculer sa puissance
---------------
Mon feedback
Marsh Posté le 21-12-2007 à 08:35:08
ReplyMarsh Posté le 23-12-2007 à 02:36:15
drap'
Qq il y a de spécial à 50hz?
Matlab serait pas plus adapté pr ce genre du choses, ou t'as vraiment besoin de Java ?
---------------
Voir les RAW sous Android: https://market.android.com/details? [...] .RawVision Blog Photo: http://photouch.me Applications mobiles: http://caketuzz.com Wapcam Project: http://wapcam.mobi
Marsh Posté le 23-12-2007 à 19:04:19
| wapcamer a écrit : drap' |
réseau électrique ?
---------------
What if I were smiling and running into your arms? Would you see then what I see now?
Marsh Posté le 23-12-2007 à 19:05:08
| sarsipius a écrit : je cherche juste à faire une fft... il n'y a pas grand chose de spécifique |
et ça :
http://www.cs.princeton.edu/introc [...] .java.html
---------------
What if I were smiling and running into your arms? Would you see then what I see now?
Marsh Posté le 24-12-2007 à 10:22:52
Je ne vois pas l'intérêt de faire une FFT pour un seul coefficient (l'harmonique en l'occurrence).
Autant calculer ce coefficient directement
Marsh Posté le 27-12-2007 à 09:49:49
ReplyMarsh Posté le 29-12-2007 à 11:03:29
ça me paraissait pourtant clair vu ce que j'ai expliqué dans le topic de tête : évaluer la puissance du pic à 50Hz
si tu peux me le calculer sans passer par une FFT dis moi comment faire ? ![]()
---------------
Mon feedback
Marsh Posté le 29-12-2007 à 11:08:38
| sarsipius a écrit : ça me paraissait pourtant clair vu ce que j'ai expliqué dans le topic de tête : évaluer la puissance du pic à 50Hz |
Ca voudrias dire que tu as un signal déjà un signal en watt comme unité en entrée, ce dont je doute, je voulais dire physiquement c'est quoi l'expérience, c'est quoi le capteur ? Il vient d'où le signal ?
Sinon c'est quoi ton niveau en maths ? Est-ce que tu sais ce qu'est (à cocher):
[ ]un nombre complexe
[ ]Le module d'un nombre complexe
[ ]Une exponentielle complexe
Message édité par sligor le 29-12-2007 à 11:11:47
Marsh Posté le 02-01-2008 à 11:47:17
merci sligor mais apparemment tu ne comprends pas ce dont j'ai besoin
pendant ce temps j'ai avancé et j'ai récupéré et adapté un morceau de code me permettant de calculer une FFT
http://www.codeproject.com/KB/reci [...] print=true
j'ai un signal composé de 5000 échantillons
comme le signal qui doit être passé en entrer doit avoir un nombre d'échantillons égal à une puissance de 2, je passe les 4096 premiers échantillons
je récupère donc 4096 valeurs après calcul de la FFT et ce que je ne comprends pas c'est le lien avec les fréquences...
je pensais que j'obtiendrais quelque chose avec en abscisses les fréquences en Hz et en ordonnées les puissances en dB mais apparemment ce n'est pas le cas
comment je peux passer de mes 4096 valeurs calculées avec les FFT à des valeurs en dB en fonction des fréquences ?
merci
---------------
Mon feedback
Marsh Posté le 02-01-2008 à 11:51:51
| sarsipius a écrit : merci sligor mais apparemment tu ne comprends pas ce dont j'ai besoin |
Répond à mes questions, je suis désolé mais si tu ne sais pas ce que tu mesures tu ne peux pas convertir en dB. Sinon ça sert à rien de calculer 4096 valeurs alors que tu n'as besoin que d'une seule.
Marsh Posté le 02-01-2008 à 12:03:19
j'ai un signal composé de 5000 échantillons enregsitrés sur 10 secondes
je veux mesurer la "puissance" en dB du pic à 50Hz
tu ferais ça comment toi à part avec Fourier ?!
et sinon à tes 3 questions je réponds positivement...
---------------
Mon feedback
Marsh Posté le 02-01-2008 à 12:58:57
| sarsipius a écrit : j'ai un signal composé de 5000 échantillons enregsitrés sur 10 secondes |
Ton signal c'est un son numérique si j'ai bien compris.
Tu fais du Fourrier que sur une seule fréquence, pas la peine de s'emmerder avec de la FFT, la transformée de Fourier discrète est aussi rapide pour calculer un unique coefficient et en plus elle est beaucoup plus simple.
http://fr.wikipedia.org/wiki/Trans [...] cr%C3%A8te
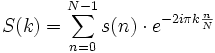
Tu n'a donc qu'à calculer S(k) pour k=50*N/(fréquence d'échantillonage) (il y a une simplification avec les N dans la formule dessous)
Choisis N de façon à avoir k entier, le plus grand possible pour avoir une meilleure précision mais cela demande une mesure plus longue (a toi de faire le choix entre précision/nombre d'échantillons qui te convient)
Pour avoir la puissance tu prends le module de (S(k)/N)
Pour convertir en dB c'est 20log(module(S(j)/N)) + A
Avec A une constante qui permet de définir ton niveau 0 ( et oui le dB est une unité relative)
Marsh Posté le 02-01-2008 à 13:36:19
non il ne s'agit pas d'un son numérique mais peu importe
le N est fixe et je ne peux pas le modifier... il est à 500Hz
je vais essayer ce que tu me proposes là
merci
---------------
Mon feedback
Marsh Posté le 02-01-2008 à 13:39:45
| sarsipius a écrit : non il ne s'agit pas d'un son numérique mais peu importe |
Attention N c'est le nombre d'échantillons(sans unité), ce n'est pas la fréquence d'échantillonage F !
Message édité par sligor le 02-01-2008 à 13:39:58
Marsh Posté le 02-01-2008 à 16:53:17
ReplyMarsh Posté le 03-01-2008 à 08:33:30
j'ai encore une question concernant la FFT pour ne pas rester bête
quand j'utilise le lemme de Danielson-Lanczos pour calculer la FFT je récupère 4096 valeurs puisque je fournis en entrée 4096 échantillons
comment je peux passer au spectre en fréquence/dB ?
ça doit être en fonction de la fréquence d'échantillonnage et du nombre d'échantillons mais je ne trouve rien à ce sujet...
---------------
Mon feedback
Marsh Posté le 04-01-2008 à 22:06:10
tu fais -20log(ordonnée) et tu as la puissa,ce en dB
---------------
Voir les RAW sous Android: https://market.android.com/details? [...] .RawVision Blog Photo: http://photouch.me Applications mobiles: http://caketuzz.com Wapcam Project: http://wapcam.mobi
Marsh Posté le 05-01-2008 à 10:11:32
ReplyMarsh Posté le 07-01-2008 à 19:01:38
| sarsipius a écrit : j'ai encore une question concernant la FFT pour ne pas rester bête |
Tu à 4096 valeurs S(k) avec k=0..4095
k=frequence*(Nombre d'échantillon)/(fréquence d'échantillonage)
donc dans ton cas frequence=k*(frequence d'échantillonage)/4096
Aprés ta valeur en db=-20log(S(k))+Constante ou db=-10log(S(k))+Constante, selon ce que tu mesures (mais comme tu ne veux pas le dire je ne pas pas t'aider pour ça), la constante dépends également ce que tu mesures car il y a plein de sous unité de mesure du decibel, je te laisse regarder cette section pour t'en convaincre:
http://en.wikipedia.org/wiki/Decib [...] asurements
Marsh Posté le 01-02-2008 à 21:08:32
La FFT calcule, si je ne m'abuse, une suite de puissance pour chaque intervalle de fréquence, mais sa valeur est *complexe*. Il faut d'abord convertir ça en module avant d'en prendre le log.
Ensuite les décibels sont toujours mesurés par rapport à une puissance unitaire: ils mesurent un ratio entre deux puissances. Suivant la puissance de base du signal, P0, le rapport P/P0 est celui dont on prend le logarithme, ce qui fait que les bels (et décibels, dix fois la valeurs en bels) diffèrent d'une constante.
Enfin la puissance P (module de la valeur complexe de FFT) dépend à l'intervalle entre les fréquences, avec un cofacteur dont il faut adapter l'effet: essayez en prenant moitié moins d'échantillon sur un signal sinusoïdal pur et vous verrez l'effet que cela peut avoir sir la fréquence d'échantillonngag n'est pas alignée sur un multiple exact de la fréquence réelle du signal pur. Il y a une correction à apporter pour en déduire la puissance réelle (estimée selon une moyenne car la phase n'est pas connue et est fixée arbitrairement par l'échantillonnage). En pratique cela veut dire que la FFT minor légèrement la puissance réelle, et d'autant plus que le nomber d'échantillon est insuffisant: la marge d'erreur est élevée pour les dernières valeurs de la FFT correspondant aux fréquences les plus hautes qui sont les plus atténuées et dont la mesure de puissance est la plus imprécise. Si l'échantillonnage est fait à 500 hertz, les puissances obtenues au dela de 250 Hz n'ont aucune signification.
Mais besoin de faire une FFT complète pour mesurer une seule composante: on fait seulement le produit du signal (modulation) avec deux sinusoïdes pures à 50Hz en décalage de phase de 90°, et on somme le tout. Des deux composantes obtenues qui forment une puissance complexe, on prend le module puis le logarithme.
Le logarithme du module est celui d'une racine carré, c'est équivalent à diviser par deux le logarithme de le somme des carrés des deux amplitudes moyennes calculées sur chacun des deux signaux modulés (sachant aussi qu'un signal mesuré a une puissance qui est elle même un carré et dont le log est double par rapport à l'amplitude du signal).
Si on neprend qu'une seule composante et pas la seconde, on ignore le déphasage possible entre le signal mesuré et la fréquence d'échantillonnage ; l'erreur sera grossière: la puissance mesurée (comme c'est le cas des transformées en sinus ou en cosinus) en dB sera presque toujours trop faible, sauf rare exception.
Maintenant faites votre choix mais sachez ce que vous voulez mesurer: puissance réelle, puissance en phase, puissance en déphasage, puissance moyenne amortie, puissance instantanée. D'ailleurs la puissance elle-même (carré d'uen amplitude) n'est pas forcément ce qu'on cherche.
Message édité par verdy_p le 01-02-2008 à 21:09:16
Marsh Posté le 01-02-2008 à 21:17:54
Optimisation possible: 5000 échantillons sur 10 secondes, la fréquence d'échantillonnage 500 Hz est un multiple exact de la composante à mesurer à 50Hz: tous les 10 échantillons on refait le même cycle sur les deux composantes à 50 hertz. Tracez les 10 points sur un cercle unitaire, on voit tout de suite les symétries: il est possible de faire la somme directe des échantillons tous les 10 échantillons, pour n'avoir plus que 10 valeurs puis seulement de multiplier par un sinus ou cosinus (et encore: il y a des symétries, il sufit d'ajouter ou retrancher entre elles les sommes avant de faire le produit, comme on factise une somme avec un facteur commun.
Donc 5 multiplications complexes au maximum, moins en fait car il y a des éléments nuls si on met deux des 10 points du cercle unitaire sur un des axes, puisque'il est permis de prendre un déphasage arbitraire avant la modulation. Avec ces optimisations, on fait ce que la FFT cherche à réaliser simultanément sur tous les autres coefficients dont on n'a pas besoin ici.
Message édité par verdy_p le 01-02-2008 à 21:49:24
Sujets relatifs:
- [C++] [résolu] Besoin d'un coup de main pour déboguer mon algo de tri
- algorithme:arbre binaire de recherche
- [JAVA]Algorithme de calcul de la limite de la somme des entiers
- Algorithme par séparation et évaluation
- [STL] Algorithme pour la valeur la plus fréquente d'un conteneur ?
- Algorithme parallélisé: Je n'arrive pas à l'écrire avec fork()
- [java] algorithme du simplexe
- Algorithme Monte Carlo
- défi algorithme date
- algorithme de gauss

Marsh Posté le 20-12-2007 à 16:32:04
salut tout le monde
Je commence sérieusement à désespérer de trouver un jour comment faire et je viens solliciter votre aide
J'ai besoin d'identifier la puissance de l'harmonique à 50Hz d'un signal
Je pensais le faire facilement avec la FFT mais je n'y comprends rien !
Est-ce que quelqu'un pourrait m'indiquer une libraire facilement utilisable pour faire une FFT ?
Merci de votre aide
---------------
Mon feedback