Le nombre d'or
Le nombre d'or - Sciences - Discussions
Marsh Posté le 06-10-2004 à 08:28:35

---------------
99 problems prick... Don't become the 100 one...
Marsh Posté le 06-10-2004 à 08:39:18
| bleup a écrit : le nombre d'or: 1,618 033 988 749 894 848 |
![[:aloy] [:aloy]](https://forum-images.hardware.fr/images/perso/aloy.gif)
Après le nombre d'or "transcendant" (« Cest cette spirale, gouvernée par un nombre transcendant (le fameux nombre dor) »), voici le nombre d'or avec un développement décimal fini.
Mesdames & Messieurs, HFR est véritablement le lieu de révolutions de grande ampleur ![[:yaisse2] [:yaisse2]](https://forum-images.hardware.fr/images/perso/yaisse2.gif)
Message édité par Profil supprimé le 06-10-2004 à 08:40:33
Marsh Posté le 06-10-2004 à 08:42:28
c est koi exactement ta question ?
desolé, mais j ai du mal a trouver un interet a ce topic. Parler d un chiffre ?
prend ce nombre et dors
---------------
#mais-chut ᓚᘏᗢ
Marsh Posté le 06-10-2004 à 08:49:43
| Z_cool a écrit : c est koi exactement ta question ? |
Etoffer le sujet sur le nombre d'or ! Ca ne sert pas à cela un forum ?
C'est un nombre très intéressant.. si tu vois pas l'intérêt passe ton chemin.
Marsh Posté le 06-10-2004 à 08:51:25
| Stephen a écrit :
|
Oui c'est comme PI.
Ici le nombre d'or calculé à 5000 décimales:
http://trucsmaths.free.fr/telech/phi_5000.zip
(bon ca sert à rien)
Marsh Posté le 06-10-2004 à 09:00:22
| bleup a écrit : Etoffer le sujet sur le nombre d'or ! Ca ne sert pas à cela un forum ? |
Je t'en prie, commence !
---------------
Ratures - Cuisine
Marsh Posté le 06-10-2004 à 09:07:17
La transcription géométrique est trés interessante aussi .
Qui s'y frotte (s'y pique) ?
Marsh Posté le 06-10-2004 à 09:07:26
| Prems a écrit : Je t'en prie, commence ! |
avec ton pseudo, c est ki devrait commencer ![]()
---------------
#mais-chut ᓚᘏᗢ
Marsh Posté le 06-10-2004 à 09:12:11
On le désigne par la lettre grecque ( phi ) en hommage au sculpteur grec Phidias (né vers 490 et mort vers 430 avant J.C) qui décora le Parthénon à Athènes. C'est Théodore Cook qui introduisit cette notation en 1914.
En fait un gars a construit son temple au hasard. Et des gens on trouvé une approximation aux proportions des son travail, et comme ils trouvaient ça cool, ils l'ont conservée.
Message édité par Prems le 06-10-2004 à 09:13:21
---------------
Ratures - Cuisine
Marsh Posté le 06-10-2004 à 09:17:30
Je n'ai pas vérifié mes dires mais je ne fais qu'apporter matière à débattre (vu que certains insistent ![]() ).
).
Le nombre d'or se retrouverait dans le rapport entre chaque côté de la base des pyramides d'Egypte et leur hauteur. Est-ce vraiment le cas? Si oui, les égyptiens connaissaient-ils cette formulation? A priori, non. Quel concept les a amenés à découvrir ce rapport si particulier... C'est là que je me dis que je devrais reprendre a lecture de L'Histoire Universelle des Chiffres, il y a peut-être la réponse dedans.
D'autre part, j'ai entendu dire qu'il y aurait ce même nombre caché dans des spirales et des fractales naturelles (style les branches d'arbre, par exemple). Là encore, est-ce vrai? Sur quelle loi naturelle repose alors le nombre d'or??
Voilà, bon débat! ![]()
Marsh Posté le 06-10-2004 à 09:18:07
Au XIXème siècle : Adolf Zeising (1810-1876), docteur en philosophie et professeur à Leipzig puis Munich, parle de "section d'or" (der goldene Schnitt) et s'y intéresse non plus à propos de géométrie mais en ce qui concerne l'esthétique et l'architecture. Il cherche ce rapport, et le trouve (on trouve facilement ce qu'on cherche ...) dans beaucoup de monuments classiques. C'est lui qui introduit le côté mythique et mystique du nombre d'or.
---------------
Ratures - Cuisine
Marsh Posté le 06-10-2004 à 09:21:19
surtout que 1.618...., c'est vaguement 3/2 qui est de base une proportion "agreable" ... y a rien de phantasmagorique la dedans.
Marsh Posté le 06-10-2004 à 09:41:38
| Prems a écrit : Au XIXème siècle : Adolf Zeising (1810-1876), docteur en philosophie et professeur à Leipzig puis Munich, parle de "section d'or" (der goldene Schnitt) et s'y intéresse non plus à propos de géométrie mais en ce qui concerne l'esthétique et l'architecture. Il cherche ce rapport, et le trouve (on trouve facilement ce qu'on cherche ...) dans beaucoup de monuments classiques. C'est lui qui introduit le côté mythique et mystique du nombre d'or. |
Je me doutais bien qu'on pourrait trouver ce rapport de manière approximative partout où on le cherche un peu. Et comme le dit Joel F, c'est proche de 1,5.
De toute façon, vu le manque de précision des constructeurs (ce n'est pas un défaut mais on ne peut pas mesurer un nombre transcendant), on pourra trouver plusieurs significations à ces faits cités.
C'est comme pour certains fameux attentats et le fait qu'on veuille retrouver le 9 et le 11 partout pour donner un sens...
Finalement, il semblerait qu'il ne reste plus au Nombre d'Or que sa signification mathématique. Il y a là plusieurs aspects intéressants dont ceux cités sur la page:
http://trucsmaths.free.fr/nombre_d_or.htm
Comme par exemple, le rapport entre phi et pi: 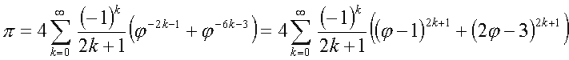
Marsh Posté le 06-10-2004 à 11:19:55
Il aurait fallu commencer par parler de l'origine, c'est a dire des proportions géométriques.
C'est bien expliqué ici:
http://www.cssh.qc.ca/projets/carn [...] re_or.html
Marsh Posté le 06-10-2004 à 16:57:49
Notons que le nombre d'or est aussi le rapport entre la taille totale et la taille des pieds au nombril pour homme parfait (ou une femme parfaite)
[HS]Pourquoi des esprits chagrins postent ils toujours des réponses agressives ???? keep cool !!! [/HS]
---------------
http://jkphoto.fr
Marsh Posté le 06-10-2004 à 22:49:50
| lechimistefou a écrit : Notons que le nombre d'or est aussi le rapport entre la taille totale et la taille des pieds au nombril pour homme parfait (ou une femme parfaite) |
dailleur il me semble que laetitia casta "respecte" ces proportions ![]()
---------------
LoD 4 ever && PWC spirit|Le topak de l'iMP-450|inDATOUNEwe trust
Marsh Posté le 06-10-2004 à 23:01:08
IWHFP ![]()
Comme le dit lechimistefou, ces proportions sont retrouvées à deux décimales près dans le corps humain, ce qui peut difficilement etre attribué au hasard, quand meme.
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 06-10-2004 à 23:05:29
ReplyMarsh Posté le 06-10-2004 à 23:11:26
| jm1981 a écrit : le nombre d'or est partout |
tiens, dis mois deux nombres au hasard.
N'importe lesquels. ![]()
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 06-10-2004 à 23:12:04
ReplyMarsh Posté le 06-10-2004 à 23:19:28
| jm1981 a écrit : 4, 15 |
4
15
19 (somme des deux précédents)
34
53
87
140
227
367
594
961
1555
Et si tu divise le dernier par le précédent...? ![]()
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 06-10-2004 à 23:25:18
| tailindil a écrit : 4 |
hin hin hin
Marsh Posté le 07-10-2004 à 08:06:12
ReplyMarsh Posté le 07-10-2004 à 08:09:47
| Prems a écrit : Au XIXème siècle : Adolf Zeising (1810-1876), docteur en philosophie et professeur à Leipzig puis Munich, parle de "section d'or" (der goldene Schnitt) et s'y intéresse non plus à propos de géométrie mais en ce qui concerne l'esthétique et l'architecture. Il cherche ce rapport, et le trouve (on trouve facilement ce qu'on cherche ...) dans beaucoup de monuments classiques. C'est lui qui introduit le côté mythique et mystique du nombre d'or. |
Rien à ajouter... ![]()
---------------
If I could start again, a million miles away, I would keep myself, I would find a way... "Loreleï's dead ; Heaven is about to fuzz."
Marsh Posté le 07-10-2004 à 09:14:10
| tailindil a écrit : IWHFP |
Le problème, c'est que à deux décimales près tu peux remettre en cause la définition rationelle (sous forme de fraction) de ce fameux nombre d'or.
---------------
Ratures - Cuisine
Marsh Posté le 07-10-2004 à 18:52:40
| Prems a écrit : Le problème, c'est que à deux décimales près tu peux remettre en cause la définition rationelle (sous forme de fraction) de ce fameux nombre d'or. |
ouais enfin ca fait bcp de hasards dans le monde alors hein ![]()
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 07-10-2004 à 18:53:31
| jm1981 a écrit : Oh ... my ... god |
ahhh oui aussi.
prends un Pentagone régulier de côté 1. A ton avis, quelle est la longueur d'un diagonale du pentagone? ![]()
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 07-10-2004 à 18:55:09
c'est bizarre tailindil , que tu aime bien le nombre d'or !
Il est directement relié à l'architecture et à la géométrie ! ![]()
![]()
![]()
Marsh Posté le 07-10-2004 à 18:57:18
| tailindil a écrit : ahhh oui aussi. |
la diagonale d'un pentagone... ![]()
---------------
Fumer tue. Ouais. Vivre aussi
Marsh Posté le 07-10-2004 à 18:59:02
ReplyMarsh Posté le 07-10-2004 à 18:59:45
| Le penseur fou a écrit :
|
c'est peut-être un adorateur de Fibonacci hein ![]()
---------------
Fumer tue. Ouais. Vivre aussi
Marsh Posté le 07-10-2004 à 19:20:17
| tristanf a écrit : la diagonale d'un pentagone... |
tu m'as bien conprit ![]()
Message édité par tailindil le 07-10-2004 à 19:20:45
---------------
La raison de vivre de la la Philosophie est de nuire à la bêtise [Nietzsche]
Marsh Posté le 07-10-2004 à 19:24:31
| Le penseur fou a écrit :
|
![]()
Fibonacci, c'est 1 1 2 3 5 8 13 21 34 55 etc ...
---------------
www.novemberguitars.com
Marsh Posté le 07-10-2004 à 19:27:11
en tout cas, ce tomic est parti pour faire du bon tomic, en effet, on retrouve en moyenne 1,618 033 988 749 894 848 conneries par post ![]() (et c'est qu'une approximation).
(et c'est qu'une approximation).
![[:rhetorie du chaos] [:rhetorie du chaos]](https://forum-images.hardware.fr/images/perso/rhetorie du chaos.gif)
---------------
Don't fuck me, I'm anonymous.
Marsh Posté le 07-10-2004 à 19:30:41
| MossieurPropre a écrit :
|
la suite qu'il a fit aussi, celle que tu a mis est la principale mais toutes celles qui suivent le même principe de construction "aboutissent" toutes au même résultat
---------------
Fumer tue. Ouais. Vivre aussi
Marsh Posté le 07-10-2004 à 19:31:46
ReplyMarsh Posté le 07-10-2004 à 19:32:32
| MossieurPropre a écrit :
|
J'aurais du dire: "le prncipe de fibonacci"
Marsh Posté le 07-10-2004 à 19:33:31
| E-Nyar a écrit : en tout cas, ce tomic est parti pour faire du bon tomic, en effet, on retrouve en moyenne 1,618 033 988 749 894 848 conneries par post |
Et pour mesurer la connerie tu t'y connais! ![]()
Sujets relatifs:
- Les pages jaunes - Nombre de parution ?
- [TopikUnik]Mystification Bogdanov, theme: Le nombre d'Or
- Machine expresso : Faut il privilegier le nombre de bar ?
- appartement et nombre de pieces....
- le nombre x=99^100
- [logic] trouver le nombre suivant...
- Evolution du nombre d'internaute en France ???
- nombre d utilisateurs élevé...
- [Recyclage] Que signifie le nombre au mileu des 3 flèches ?
- [Topikunik] Enigmes. 64 enigmes. NEW: Plus petit nombre par Welkin

![[:totoz] [:totoz]](https://forum-images.hardware.fr/images/perso/totoz.gif)
Marsh Posté le 06-10-2004 à 08:19:07
le nombre d'or: 1,618 033 988 749 894 848


Ou:
donc:
Ce nombre est une harmonie, que certains estiment parfaite, existe entre deux grandeurs, notamment entre deux dimensions, lorsque celles-ci sont entre elles dans la même proportion que la plus grande avec leur somme.